Процент. Наращение
По отношению к следующим периодам ставки процентов трактуются по-разному в зависимости от принятой схемы начисления: по простым или по сложным процентам. В первом случае приросты денежных сумм для любого периода будут составлять все ту же долю i от первоначальной суммы Р. в результате наращенная за п периодов сумма составит величину
Sn=P+n·i·P=P·(1+n·i) (1)
Здесь и в дальнейшем будем пользоваться дробным измерением ставки i.
В отличие от простых для сложных процентов одна и та же ставка i берется для каждого последующего промежутка не от первоначальной суммы, а от результата предыдущего начисления, т.е. от суммы, наращенной на начало данного периода. Отсюда следует, что вклад Р при ставке сложного процента i через п периодов составит сумму
Sn=P·(1+i)n (2)
Таким образом, последовательность наращенных сумм {Sn} в случае простых процентов представляет арифметическую прогрессию, в то время как для сложных процентов прогрессия будет геометрической.
Выражения (1) и (2) называют формулой простых и, соответственно, сложных процентов, а под процентными деньгами или, кратко, процентами понимают величину дохода (приращение денег) In=Sn-P. В финансовых вычислениях в случае меняющихся во времени процентных ставок используют очевидные обобщения правил (1), (2):
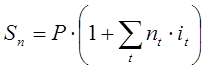- для простых процентов,
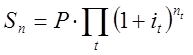- для сложных процентов.
Дисконтирование и удержание процентов. Эти процедуры являются обратными по отношению к процессу начисления процентов. Дисконтированием называется авансовое удержание с заемщика процентов в момент выдачи ссуды, т.е. до наступления срока ее погашения.
Другим вариантом дисконтирования является учет векселей в банке, когда банк, принимая вексель от предъявителя, выдает ему обозначенную на векселе сумму до срока ее погашения. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока погашения. Подобным образом (с дисконтом) государство продает большинство своих ценных бумаг (долговых обязательств).
В нашем случае исходной величиной выступает не начальный вклад Р, а некоторая будущая сумма S. Вопрос состоит в том, чтобы определить эквивалентную сумму Р, отстоящую на t предшествующих периодов до срока выплаты S. В зависимости от принятого критерия эквивалентности можно выделить два подхода к расчету предшествующих сумм.
Во-первых, по размеру вклада Р, который при начислении процентов через t периодов дает сумму S, и, во-вторых, по размеру платежа, к которому придем при удержании процентов с финальной суммы S за срок t. Таким образом, при одном толковании за базовую величину, т.е. за 100%, принимается размер вклада Р, в то время как при другом – за 100% берется будущая сумма S. Кроме того, по каждому варианту дисконтирование можно производить как по простым, так и по сложным процентам.
В случае приведения по вкладу Р для нахождения дисконтированных значений достаточно воспользоваться формулами (1) и (2), решив их относительно величины Р.
Еще о комерческих банках:
Структура портфеля в разрезе страховых услуг
При анализе АО «Альянс-полис», можно отметить, что ситуация на банковском секторе отразилась, как на общем страховании, так и на отрасли «страхование жизни». При этом динамика роста последней остается положительной за счет роста аннуитетного страхования. В отрасли «страхование жизни» сбор страховых ...
Проблемы ипотечного кредитования
Отечественная ипотека, в отличие от зарубежной, обоснованно расценивалась экспертами как надежный и эффективный финансовый инструмент. Выдаче ипотечных кредитов предшествовали тщательная проверка платежеспособности заемщика и предоставление солидного пакета документов. Поэтому с полным правом можно ...
История создания, организация деятельности Федеральной Службы по
Финансовому рынку
Город Москва является исторически сложившимся культурным, политическим и туристическим центром, столицей Российской Федерации. Москва расположена в центре европейской части России, в междуречье Оки и Волги, на 55° 45' северной широты и 37° 37' восточной долготы, на реке Москве, в среднем на высоте ...
Навигация
- Главная
- Коммерческие банки
- Банковские кризисы
- Операции с ценными бумагами
- Операции банков с векселями
- Зарождение института страхования
- Роль и границы кредита
- Экономика